Science Memes

15735 readers

3601 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

316

Wake up babe new shape just dropped (sopuli.xyz)

submitted 5 days ago by [email protected] to c/[email protected]

31 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 37 points 5 days ago (2 children)

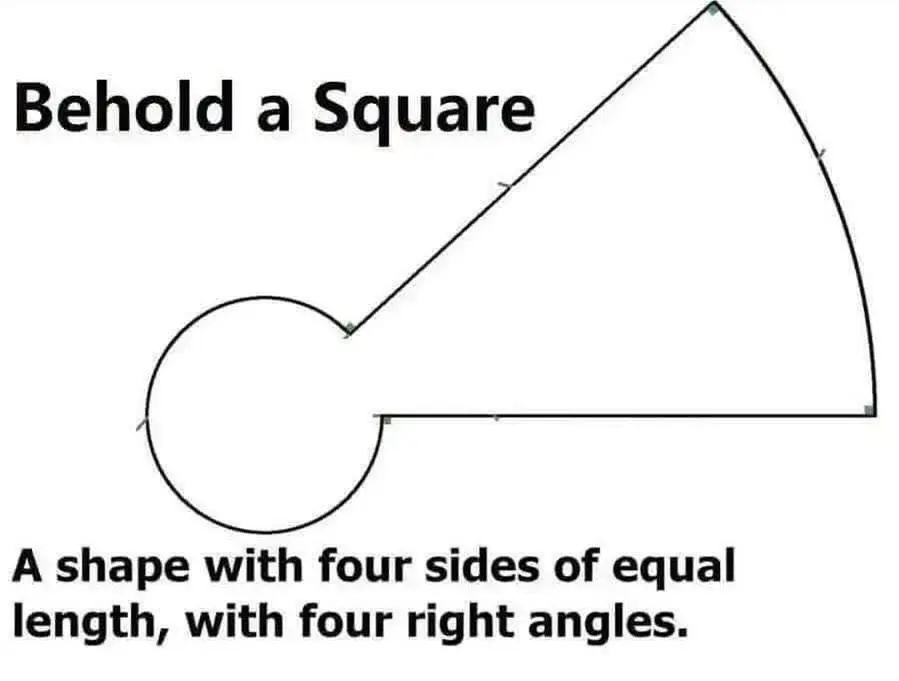
I don’t remember all my geometric rules I guess, but can an arc, intersecting a line, ever truly be a right angle? At no possible length of segment along that arc can you draw a line that’s perpendicular to the first.

[–] [email protected] 14 points 5 days ago (1 children)

An infinitely small segment of the arc can be.
Geometrically there isn't a problem. If you draw a line from that point to the center of the arc, it will make it clearer.

[–] [email protected] 5 points 5 days ago* (last edited 5 days ago)

I guess if we define it as a calculus problem, I can see the point..

I didn’t mean to pun but there it is and I’m leaving it. Any way, there is no infinitely small section that’s perpendicular. Only the tangent at a single (infinitely small) point along a smooth curve, as we approach from either direction. Maybe that’s still called perpendicular.

[–] [email protected] 5 points 5 days ago

A right angle exists between the radius of the circle and the line tangent to the circle at the point that the radial line intersects it. So we can say the radius forms a right angle with the circle at that point because the slope of the curve is equal to that of the tangent line at that point.